Løsningsforslag S2 eksamen V2023
Skrevet av Ståle Gjelsten 24. mai 2023. Jeg setter veldig pris på om du melder ifra om feil eller unøyaktigheter på forumet på matematikk.net
Del 1
Oppgave 1
Oppgave 2
2a
Når det blir produsert 40 enheter kan vi finne en tilnærmet verdi for grensekostnaden
Jeg forsøkte å legge en tangent i punktet, og fikk stigningstallet
2b
Jeg vet at overskuddet blir størst når
Det ser ut til stigningstallene er like store omtrent ved
Vi har størst overskudd ved produksjon av omtrent 55 enheter.
Oppgave 3
3a
Siden summen av sannsynlighetene skal være lik 1 må
Dermed er:
3b
| 0 | 1 | 2 | 3 | Sum | |
|---|---|---|---|---|---|
| 0,4 | 0,3 | 0,2 | 0,1 | 1 | |
| 0 | 0,3 | 0,4 | 0,3 | 1 | |
| 0,4 | 0 | 0,2 | 0,4 | 1 |
Forventningsverdien er
Variansen er
Oppgave 4
4a
Det ser ut til at eleven forsøker å regne ut delsummer av en aritmetisk rekke. Helt konkret ser det ut til at eleven forsøker å regne ut summen av de ti første leddene når startverdien er 3 og differansen er 4, altså
4b
Vi kan finne summen av denne aritmetiske rekka med:
Oppgave 5
Den første dagen får Knut tilført 7 mg virkestoff, andre dag så er mengden virkestoff redusert til
På dag
Dette er en geometrisk rekke som konvergerer når
Mengden virkestoff hos Knut vil aldri overstige 70 mg. Legens påstand er riktig.
Oppgave 6
6a
Siden vi skal finne
6b
Sannsynligheten for at levetiden er kortere enn
Det er 75,8 % sannsynlighet for at et tilfeldig valgt batteri har levetid mer enn 465 timer.
6c
Siden forventningsverdien er 500 må toppunktet til normalfordelingsfunksjonen ligge ved
I tillegg vet vi at standardavviket er 50. Hvis vi beveger oss et standardavvik mot høyre eller venstre fra forventningsverdien skal vi komme til vendepunktene til normalfordelingsfunksjonen. Det ser ut til å stemme bra med graf A, hvor vendepunktene ligger ved omtrent
Graf A illustrerer
Del 2
Oppgave 1
1a
Annuitetslån har faste terminbeløp slik at lånebeløpet er lik produktet terminfaktoren multiplisert med terminbeløpet:
Vi kan beregne terminfaktoren
Og terminbeløpet blir da
Terminbeløpet er 4555,14 kr.
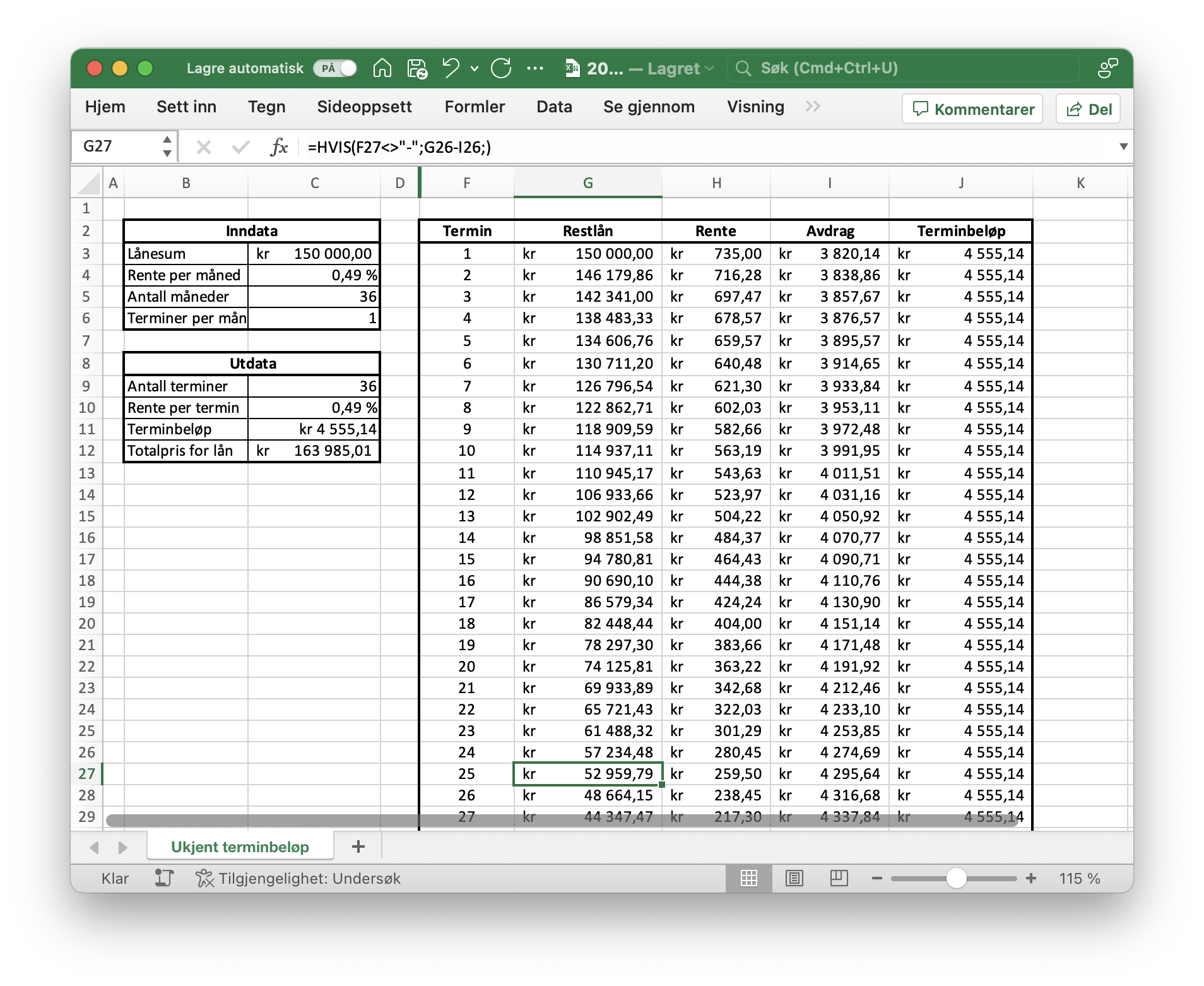
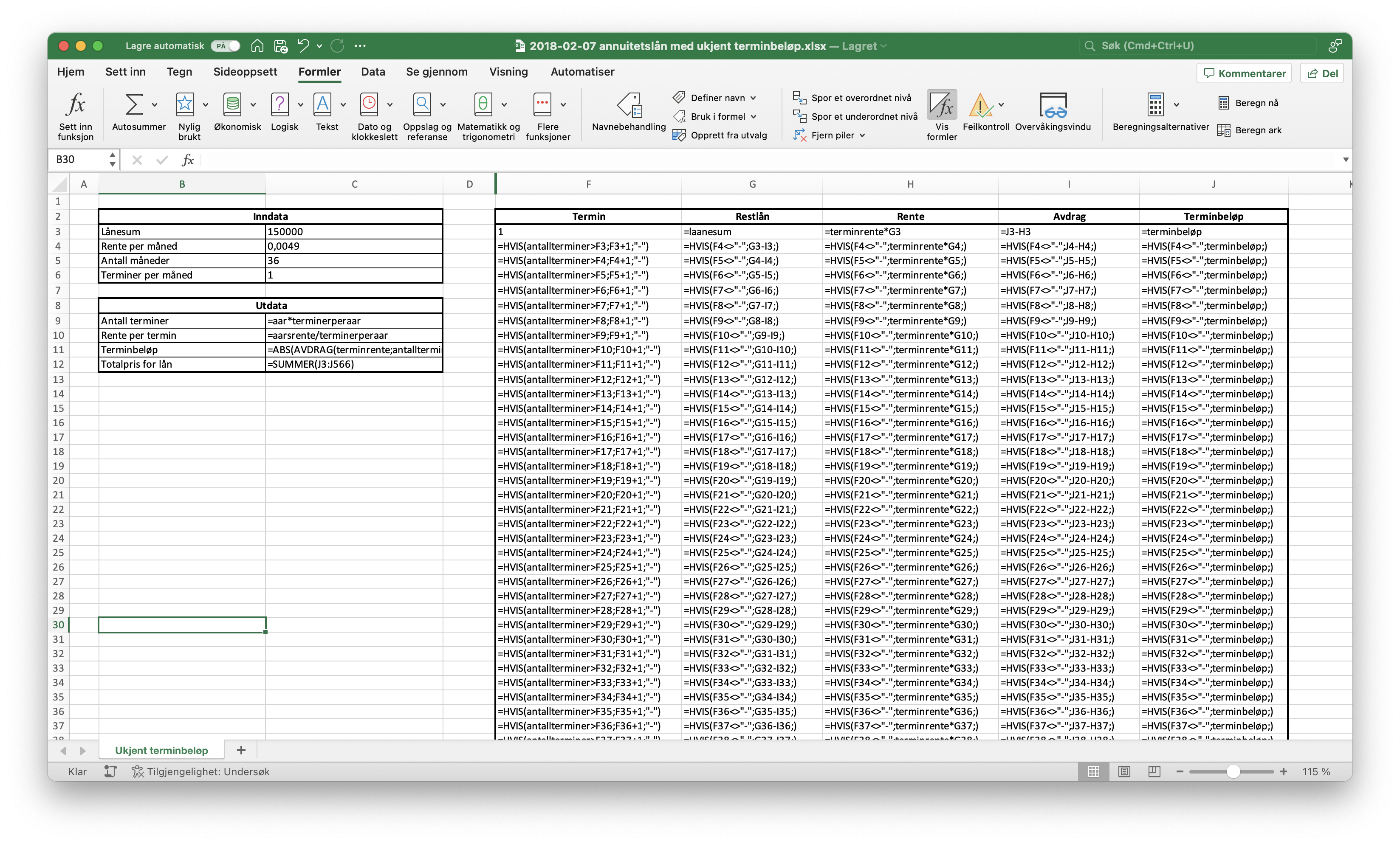
1b
Jeg bruker en ferdig regnearkmodell jeg hadde liggende til å løse denne oppgaven. Fra regnearket ser jeg at restlånet før 25. innbetaling er 52 959,79 kr. Dermed vil erstatningen fra forsikringsselskapet dekke restlånet (gitt at han betaler restlånet med en gang han får erstatningen). Se utklippet under.
Oppgave 2
2a
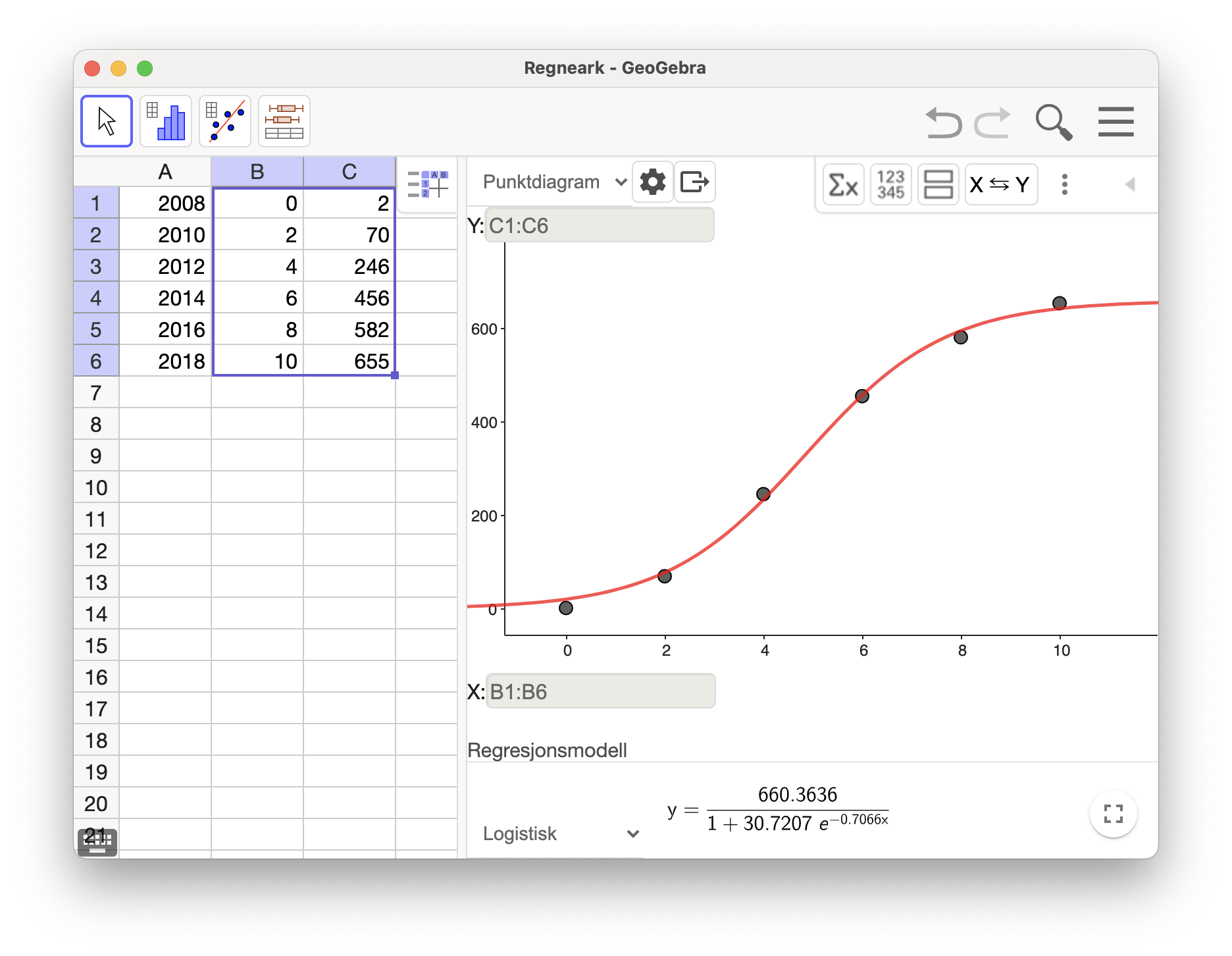
Jeg brukte regresjonsverktøyet i GeoGebra valgte den logistiske modellen:
Logistiske funksjoner flater ut ved en horisontal asymptote (i dette tilfellet 660,37 millioner kr). Selv om det kanskje høres usannsynlig ut at markedet for musikkstrømming ikke kommer til å vokse, så tror jeg at nærmest all musikklytting allerede er blitt flyttet fra formater som CD og nedlasting, til strømming. Derfor er det usannsynlig veksten kommer til å fortsette i samme tempo. En logistisk modell har også asymptote ved
Kommentar: Man kan også argumentere for andre regresjonsmodeller, f.eks. vil en tredjegradsmodell passe fint. Vær imidlertid klar over at tredjegradsmodellen sannsynligvis vil ha et mindre gyldighetsområde siden denne har negativ vekstfart både før 2008 og etter 2018. Sensorveiledninga sier at flere ulike modeller kan gi full uttelling så lenge de begrunnes godt.
2b
Se utklippet fra CAS.
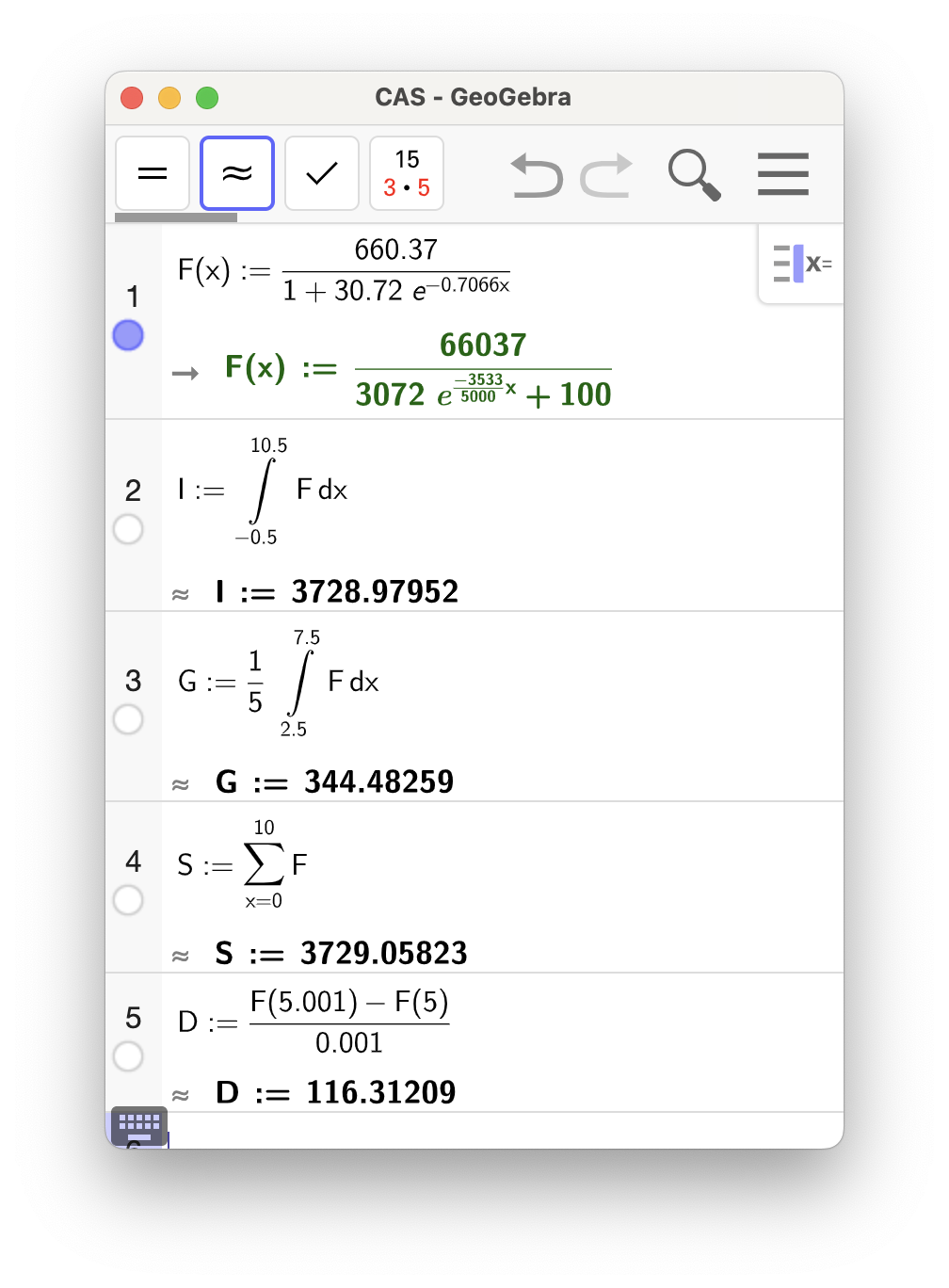
2c
Oppgave 3
3a
Vi starter med noen antagelser:
- Birger velger helt tilfeldig om han fyller hvert enkelt glass med Pepsi-Cola eller Coca-Cola
- Marte tipper helt tilfeldig for hvert colaglass
- Marte glemmer hva hun har gjettet på de forrige glassene, og smaken setter seg ikke i munnen hennes slik at vi kan anta at forsøkene er uavhengige
Vi kan da behandle dette som et binomisk forsøk med
Vi kan beregne denne sannsynligheten enkelt i GeoGebra, eller med formelen:
3b
Vi lar
Det skal mye til at Marte er dårligere til å gjenkjenne colaene enn ved tilfeldig gjetting, og jeg er egentlig kun interessert i å finne ut om hun bedre enn tilfeldig gjetning. Derfor velger jeg en ensidig hypotesetest. Vi skal bruke signifikansnivået
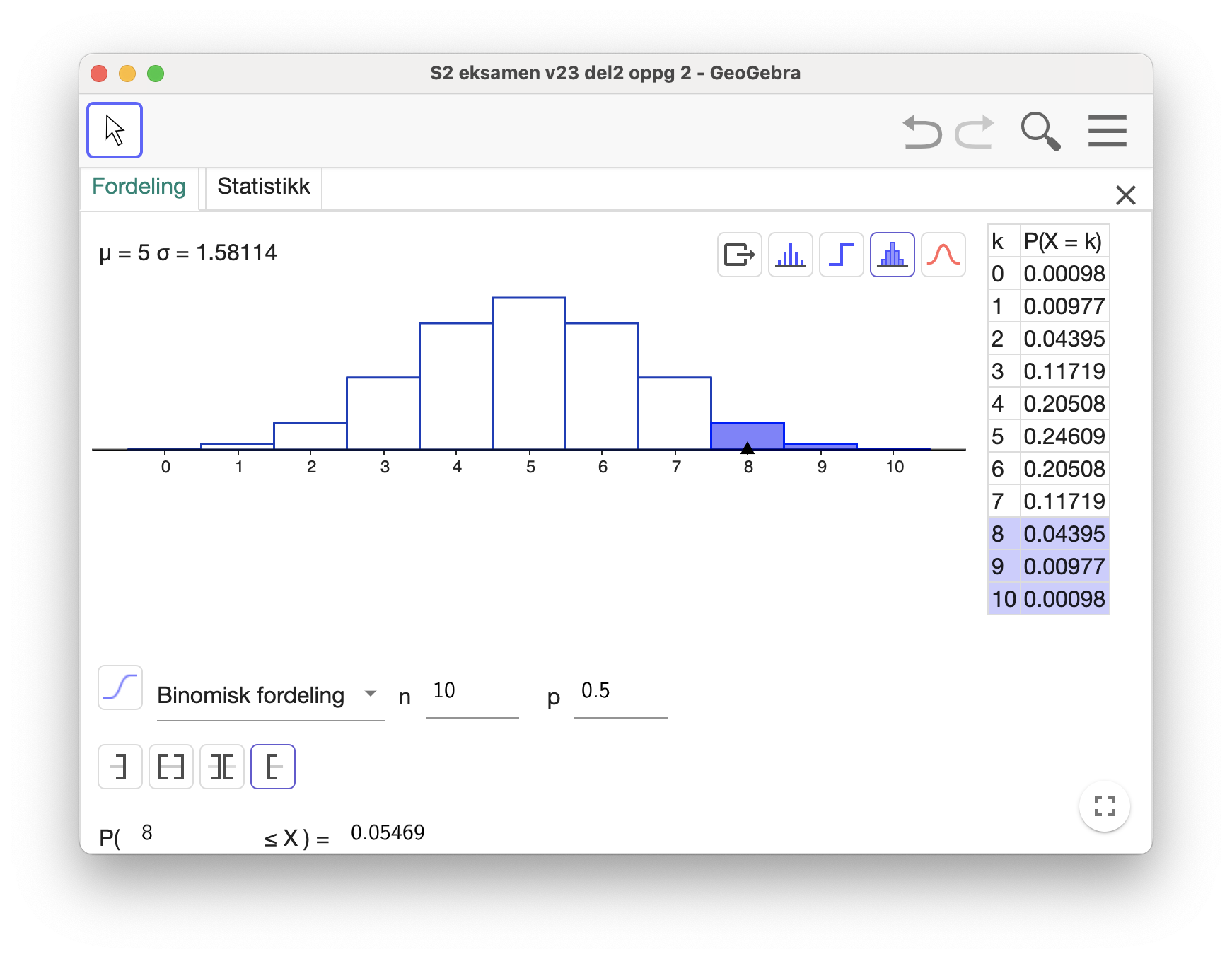
Ved hjelp av GeoGebra finner jeg at
Siden sannsynligheten
3c
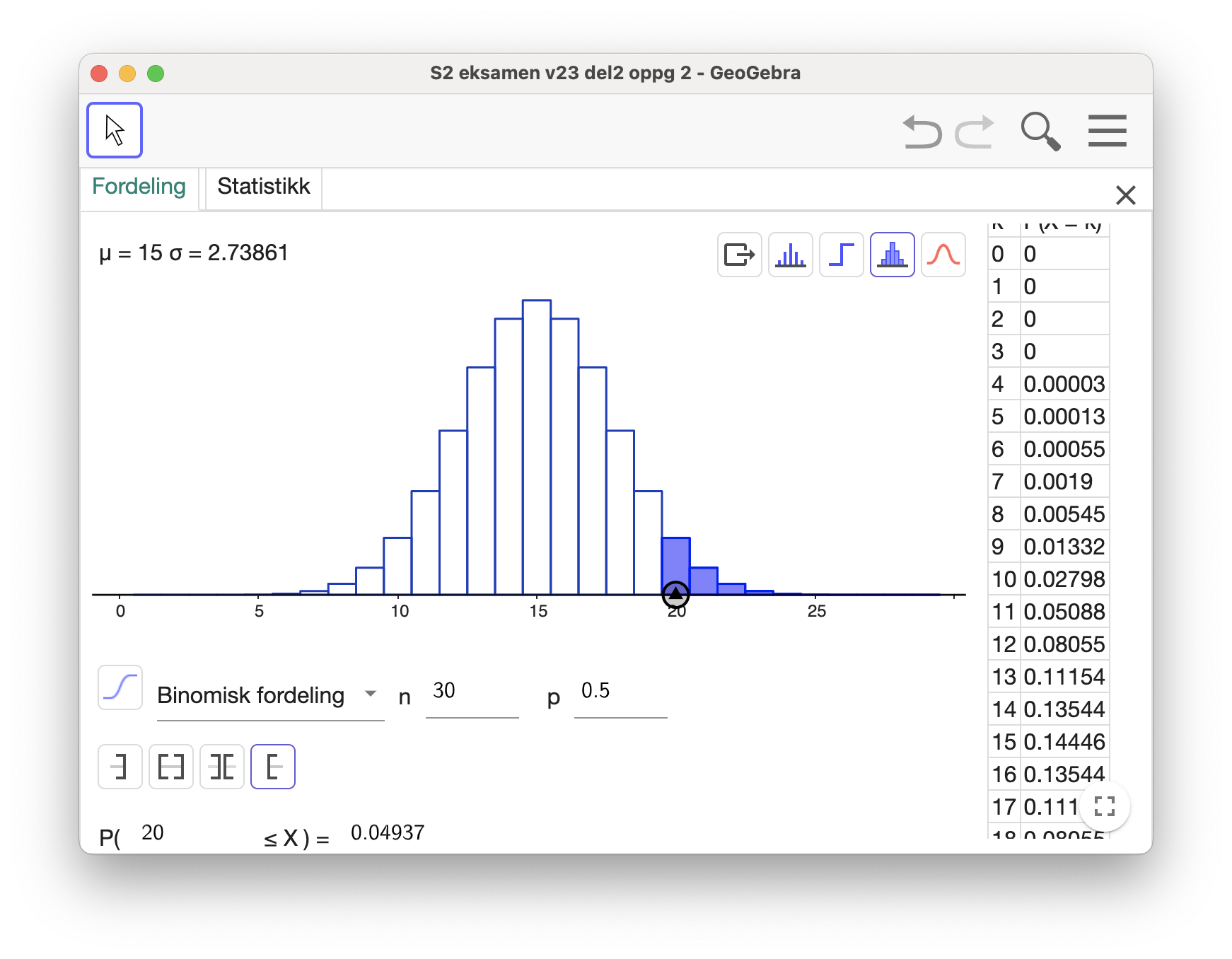
Jeg brukte sannsynlighetsverktøyet i GeoGebra og endret antallet,
Dersom Marte gjetter riktig på minst 20 glass så kan hun overbevise Birger om at hun er bedre til å gjenkjenne cola enn en tilfeldig gjetter med et signifikansnivå på 5 %.
Oppgave 4
Jeg gjorde disse oppgavene i Excel, se regnearket under.
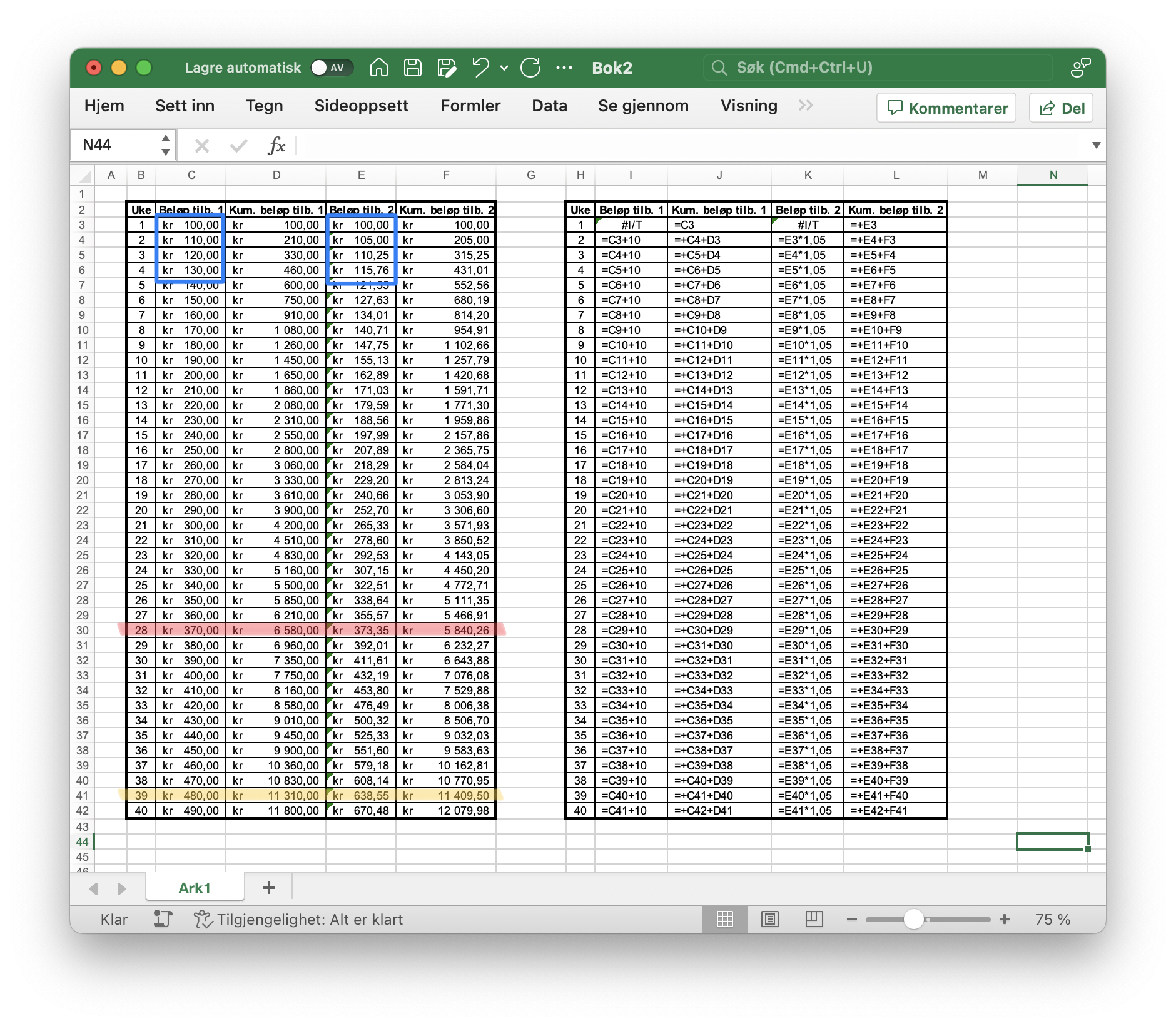
4a
De ukentlige beløpene for de fire første ukene er markert i blått i utklippet. Det venstre blå rektangelet viser beløpene for tilbud 1, det høyre blå rektangelet viser beløpene for tilbud 2. Vi kan se at tilbud 1 vokser fortere enn tilbud 2 i starten.
4b
I uke 28 så vil tilbud 2 for første gang gi større utbetaling enn tilbud 1, se den røde markering i Excel-arket.
4c
I uke 39 så vil tilbud 2 for første gang ha gitt større samlet utbetaling enn tilbud 1, se den gule markeringen i Excel-arket.
Oppgave 5
5a
Se programmet under.
from scipy.stats import norm # henter nødvendige pakker for normalfordeling
from random import randint
n = 20
sum_karakterer = 0
for i in range(n):
# trekker et tilfeldig tall fra 1 til 3. Dette tilsvarer
# skole A, B og C
skole = randint(1,3)
if skole == 1:
# hvis det tilfeldige tallet er 1, så skal vi trekke
# tilfeldig elev fra skole A. I dette tilfellet har
# normalfordelingen my = 3.8 og sigma = 1.2
# # vi trekker en tilfeldig elev med norm.rvs()
elev = norm.rvs(3.8,1.2)
elif skole == 2:
elev = norm.rvs(3.4,1.4)
else:
elev = norm.rvs(4.1,1.1)
# vi legger til elevens karakter på summen
sum_karakterer += elev
print(f"Gjennomsnittskarakteren til de {n} elevene er {sum_karakterer/n:.3f}.")
5b
from scipy.stats import norm # henter nødvendige pakker for normalfordeling
from random import randint
N = 10_000
antall_gunstige = 0
for j in range(N):
n = 20
sum_karakterer = 0
for i in range(n):
# trekker et tilfeldig tall fra 1 til 3.
# Dette tilsvarer skole A, B og C
skole = randint(1,3)
if skole == 1:
# hvis det tilfeldige tallet er 1, så skal vi trekke
# tilfeldig elev fra skole A. I dette tilfellet har
# normalfordelingen my = 3.8 og sigma = 1.2
# # vi trekker en tilfeldig elev med norm.rvs()
elev = norm.rvs(3.8,1.2)
elif skole == 2:
elev = norm.rvs(3.4,1.4)
else:
elev = norm.rvs(4.1,1.1)
# vi legger til elevens karakter på summen
sum_karakterer += elev
if sum_karakterer/n > 4:
# hvis snittkarakteren er over 4 så har vi et gunstig utfall
antall_gunstige += 1
print(f"Etter {N} simuleringer estimerer jeg at sannsynligheten for at"
f"gjennomsnittskarakteren er over 4 til {antall_gunstige/N:.4f}.")
Jeg brukte
Sannsynligheten for at gjennomsnittskarakteren til de 20 elevene er over 4 er estimert til 0,205 ved hjelp av programmet over.